

Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *...*n k .
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая - из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .
Пример 2.
Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение:
n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =...n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3.
Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение.
Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1.
Пример 5
. Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение:
т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6 . Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний обозначается C n m и вычисляется по формуле:
![]()
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
![]()
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение: эта задача о числе перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9.
На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение:
В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
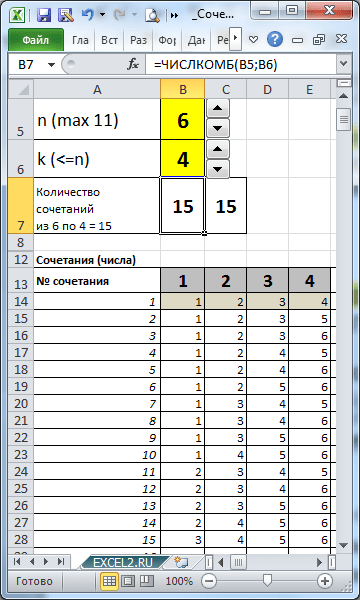
Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).
Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:
(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)
Примечание : Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье - плохая идея.
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.
Задавая с помощью количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.
Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.
Нам нужно определить число Сочетаний 7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.
КОМБИНАТОРИКА
Комбинаторика - раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В - n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье - n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
![]()
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
![]() .
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
![]() .
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
![]() .
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
![]()
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
![]()
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.

Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
![]()
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ "КОМБИНАТОРИКА"
Чтобы в материале было легче ориентироваться, добавлю содержание данной темы:
В этой теме рассмотрим основные понятия комбинаторики: перестановки, сочетания и размещения. Выясним их суть и формулы, по которым можно найти их количество.
Для работы нам понадобятся кое-какие вспомогательные сведения. Начнём с такого фундаментального математического понятия как множество. Подробно понятие множества было раскрыто в теме "Понятие множества. Способы задания множеств" .
Очень краткий рассказ про множества : показать\скрыть
Если вкратце: множеством именуют некую совокупность объектов. Записывают множества в фигурных скобках. Порядок записи элементов роли не играет; повторения элементов не допускаются. Например, множество цифр числа 11115555999 будет таким: $\{1,5,9 \}$. Множество согласных букв в слове "тигрёнок" таково: $\{т, г, р, н, к\}$. Запись $5\in A$ означает, что элемент 5 принадлежит множеству $A=\{1,5,9 \}$. Количество элементов в конечном множестве называют мощностью этого множества и обозначают $|A|$. Например, для множества $A=\{1,5,9 \}$, содержащего 3 элемента, имеем: $|A|=3$.
Рассмотрим некое непустое конечное множество $U$, мощность которого равна $n$, $|U|=n$ (т.е. в множестве $U$ имеется $n$ элементов). Введём такое понятие, как выборка (некоторые авторы именуют её кортежем). Под выборкой объема $k$ из $n$ элементов (сокращённо $(n,k)$-выборкой) будем понимать набор элементов $(a_1, a_2,\ldots, a_k)$, где $a_i\in U$. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Две упорядоченные выборки, различающиеся лишь порядком элементов, являются различными. Если порядок следования элементов выборки не является существенным, то выборку именуют неупорядоченной.
Заметьте, что в определении выборки ничего не сказано про повторения элементов. В отличие от элементов множеств, элементы выборки могут повторяться.
Для примера рассмотрим множество $U=\{a,b,c,d,e\}$. Множество $U$ содержит 5 элементов, т.е. $|U|=5$. Выборка без повторений может быть такой: $(a,b,c)$. Данная выборка содержит 3 элемента, т.е. объём этой выборки равен 3. Иными словами, это $(5,3)$-выборка.
Выборка с повторениями может быть такой: $(a,a,a,a,a,c,c,d)$. Она содержит 8 элементов, т.е. объём её равен 8. Иными словами, это $(5,8)$-выборка.
Рассмотрим ещё две $(5,3)$-выборки: $(a,b,b)$ и $(b,a,b)$. Если мы полагаем наши выборки неупорядоченными, то выборка $(a,b,b)$ равна выборке $(b,a,b)$, т.е. $(a,b,b)=(b,a,b)$. Если мы полагаем наши выборки упорядоченными, то $(a,b,b)\neq(b,a,b)$.
Рассмотрим ещё один пример, немного менее абстрактный:) Предположим, в корзине лежат шесть конфет, причём все они различны. Если первой конфете поставить в соответствие цифру 1, второй конфете - цифру 2 и так далее, то с конфетами в корзине можно сопоставить такое множество: $U=\{1,2,3,4,5,6\}$. Представьте, что мы наугад запускаем руку в корзинку с целью вытащить три конфеты. Вытащенные конфеты - это и есть выборка. Так как мы вытаскиваем 3 конфеты из 6, то получаем (6,3)-выборку. Порядок расположения конфет в ладони совершенно несущественен, поэтому эта выборка является неупорядоченной. Ну, и так как все конфеты различны, то выборка без повторений. Итак, в данной ситуации говорим о неупорядоченной (6,3)-выборке без повторений.
Теперь подойдём с иной стороны. Представим себе, что мы находимся на фабрике по производству конфет, и на этой фабрике производятся конфеты четырёх сортов. Множество $U$ в этой ситуации таково: $U=\{1,2,3,4 \}$ (каждая цифра отвечает за свой сорт конфет). Теперь вообразим, что все конфеты ссыпаются в единый жёлоб, около которого мы и стоим. И, подставив ладони, из этого потока отбираем 20 конфет. Конфеты в горсти – это и есть выборка. Играет ли роль порядок расположения конфет в горсти? Естественно, нет, поэтому выборка неупорядоченная. Всего 4 сорта конфет, а мы отбираем двадцать штук из общего потока - повторения сортов неизбежны. При этом выборки могут быть самыми различными: у нас даже могут оказаться все конфеты одного сорта. Следовательно, в этой ситуации мы имеем дело с неупорядоченной (4,20)-выборкой с повторениями.
Рассмотрим ещё пару примеров. Пусть на кубиках написаны различные 7 букв: к, о, н, ф, е, т, а. Эти буквы образуют множество $U=\{к,о,н,ф,е,т,а\}$. Допустим, из данных кубиков мы хотим составить "слова" из 5 букв. Буквы этих слов (к примеру, «конфе», «тенко» и так далее) образуют (7,5)-выборки: $(к,о,н,ф,е)$, $(т,е,н,к,о)$ и т.д. Очевидно, что порядок следования букв в такой выборке важен. Например, слова «нокфт» и «кфтон» различны (хотя состоят из одних и тех же букв), ибо в них не совпадает порядок букв. Повторений букв в таких «словах» нет, ибо в наличии только семь кубиков. Итак, набор букв каждого слова представляет собой упорядоченную (7,5)-выборку без повторений.
Еще один пример: мы составляем всевозможные восьмизначные числа из четырёх цифр 1, 5, 7, 8. Например, 11111111, 15518877, 88881111 и так далее. Множество $U$ таково: $U=\{1,5,7,8\}$. Цифры каждого составленного числа образуют (4,8)-выборку. Порядок следования цифр в числе важен, т.е. выборка упорядоченная. Повторения допускаются, поэтому здесь мы имеем дело с упорядоченной (4,8)-выборкой с повторениями.
Размещение без повторений из $n$ элементов по $k$ - упорядоченная $(n,k)$-выборка без повторений.
Так как элементы в рассматриваемой выборке повторяться не могут, то мы не можем отобрать в выборку больше элементов, чем есть в исходном множестве. Следовательно, для таких выборок верно неравенство: $n≥ k$. Количество размещений без повторений из $n$ элементов по $k$ определяется следующей формулой:
\begin{equation}A_{n}^{k}=\frac{n!}{(n-k)!} \end{equation}
Что обозначает знак "!"? : показать\скрыть
Запись "n!" (читается "эн факториал") обозначает произведение всех чисел от 1 до n, т.е.
$$ n!=1\cdot2\cdot 3\cdot \ldots\cdot n $$
По определению полагается, что $0!=1!=1$. Для примера найдём 5!:
$$ 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120. $$
Пример №1
Алфавит состоит из множества символов $E=\{+,*,0,1,f\}$. Определим количество таких трёхсимвольных слов в этом алфавите, которые не содержат повторяющихся букв.
Под трёхсимвольными словами будем понимать выражения вида "+*0" или "0f1". В множестве $E$ пять элементов, поэтому буквы трехсимвольных слов образуют (5,3)-выборки. Первый вопрос: эти выборки упорядочены или нет? Слова, которые отличаются лишь порядком букв, полагаются различными, поэтому порядок элементов в выборке важен. Значит, выборка является упорядоченной. Второй вопрос: допускаются повторения или нет? Ответ на этот вопрос даёт условие: слова не должны содержать повторяющихся букв. Подводим итоги: буквы каждого слова, удовлетворяющего условию задачи, образуют упорядоченную (5,3)-выборку без повторений. Иными словами, буквы каждого слова образуют размещение без повторений из 5 элементов по 3. Вот примеры таких размещений:
$$ (+,*,f), \; (*,+,f), \; (1,+,0) $$
Нас же интересует общее количество этих размещений. Согласно формуле (1) количество размещений без повторений из 5 элементов по 3 будет таким:
$$ A_{5}^{3}=\frac{5!}{(5-3)!}=\frac{5!}{2!}=60. $$
Т.е. можно составить 60 трёхсимвольных слов, буквы которых не будут повторяться.
Ответ : 60.
Размещение с повторениями из $n$ элементов по $k$ - упорядоченная $(n,k)$-выборка с повторениями.
Количество размещений с повторениями из $n$ элементов по $k$ определяется следующей формулой:
\begin{equation}\bar{A}_{n}^{k}=n^k \end{equation}
Пример №2
Сколько пятизначных чисел можно составить из множества цифр $\{5,7,2\}$?
Из данного набора цифр можно составить пятизначные числа 55555, 75222 и так далее. Цифры каждого такого числа образуют (3,5)-выборку: $(5,5,5,5,5)$, $(7,5,2,2,2)$. Зададимся вопросом: что это за выборки? Во-первых, цифры в числах могут повторяться, поэтому мы имеем дело с выборками с повторениями. Во-вторых, порядок расположения цифр в числе важен. Например, 27755 и 77255 - разные числа. Следовательно, мы имеем дело с упорядоченными (3,5)-выборками с повторениями. Общее количество таких выборок (т.е. общее количество искомых пятизначных чисел) найдём с помощью формулы (2):
$$ \bar{A}_{3}^{5}=3^5=243. $$
Следовательно, из заданных цифр можно составить 243 пятизначных числа.
Ответ : 243.
Перестановка без повторений из $n$ элементов - упорядоченная $(n,n)$-выборка без повторений.
По сути, перестановка без повторений есть частный случай размещения без повторений, когда объём выборки равен мощности исходного множества. Количество перестановок без повторений из $n$ элементов определяется следующей формулой:
\begin{equation}P_{n}=n! \end{equation}
Эту формулу, кстати, легко получить, если учесть, что $P_n=A_{n}^{n}$. Тогда получим:
$$ P_n=A_{n}^{n}=\frac{n!}{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n! $$
Пример №3
В морозилке лежат пять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?
Пусть первому мороженому соответствует цифра 1, второму - цифра 2 и так далее. Мы получим множество $U=\{1,2,3,4,5\}$, которое будет представлять содержимое морозилки. Порядок съедения может быть таким: $(2,1,3,5,4)$ или таким: $(5,4,3,1,2)$. Каждый подобный набор есть (5,5)-выборка. Она будет упорядоченной и без повторений. Иными словами, каждая такая выборка есть перестановка из 5 элементов исходного множества. Согласно формуле (3) общее количество этих перестановок таково:
$$ P_5=5!=120. $$
Следовательно, существует 120 порядков выбора очередности съедения.
Ответ : 120.
Перестановка с повторениями – упорядоченная $(n,k)$-выборка с повторениями, в которой элемент $a_1$ повторяется $k_1$ раз, $a_2$ повторяется $k_2$ раза так далее, до последнего элемента $a_r$, который повторяется $k_r$ раз. При этом $k_1+k_2+\ldots+k_r=k$.
Общее количество перестановок с повторениями определяется формулой:
\begin{equation}P_{k}(k_1,k_2,\ldots,k_r)=\frac{k!}{k_1!\cdot k_2!\cdot \ldots \cdot k_r!} \end{equation}
Пример №4
Слова составляются на основе алфавита $U=\{a,b,d\}$. Сколько различных слов из семи символов может быть составлено, если в этих словах буква "a" должна повторяться 2 раза; буква "b" - 1 раз, а буква "d" - 4 раза?
Вот примеры искомых слов: "aabdddd", "daddabd" и так далее. Буквы каждого слова образуют (3,7)-выборку с повторениями: $(a,a,b,d,d,d,d)$, $(d,a,d,d,a,b,d)$ и т.д. Каждая такая выборка состоит из двух элементов "a", одного элемента "b" и четырёх элементов "d". Иными словами, $k_1=2$, $k_2=1$, $k_3=4$. Общее количество повторений всех символов, естественно, равно объёму выборки, т.е. $k=k_1+k_2+k_3=7$. Подставляя эти данные в формулу (4), будем иметь:
$$ P_7(2,1,4)=\frac{7!}{2!\cdot 1!\cdot 4!}=105. $$
Следовательно, общее количество искомых слов равно 105.
Ответ : 105.
Сочетание без повторений из $n$ элементов по $k$ – неупорядоченная $(n,k)$-выборка без повторений.
Общее количество сочетаний без повторений из $n$ элементов по $k$ определяется формулой:
\begin{equation}C_{n}^{k}=\frac{n!}{(n-k)!\cdot k!} \end{equation}
Пример №5
В корзине размещены карточки, на которых написаны целые числа от 1 до 10. Из корзины вынимают 4 карточки и суммируют числа, написанные на них. Сколько различных наборов карточек можно вытащить из корзины?
Итак, в данной задаче исходное множество таково: $U=\{1,2,3,4,5,6,7,8,9,10\}$. Из этого множества мы выбираем четыре элемента (т.е., четыре карточки из корзины). Номера вытащенных элементов образуют (10,4)-выборку. Повторения в этой выборке не допускаются, так как номера всех карточек различны. Вопрос вот в чём: порядок выбора карточек играет роль или нет? Т.е., к примеру, равны ли выборки $(1,2,7,10)$ и $(10,2,1,7)$ или не равны? Тут нужно обратиться к условию задачи. Карточки вынимаются для того, чтобы потом найти сумму элементов. А это значит, что порядок карточек не важен, так как от перемены мест слагаемых сумма не изменится. Например, выборке $(1,2,7,10)$ и выборке $(10,2,1,7)$ будет соответствовать одно и то же число $1+2+7+10=10+2+1+7=20$. Вывод: из условия задачи следует, что мы имеем дело с неупорядоченными выборками. Т.е. нам нужно найти общее количество неупорядоченных (10,4)-выборок без повторений. Иными словами, нам нужно найти количество сочетаний из 10 элементов по 4. Используем для этого формулу (5):
$$ C_{10}^{4}=\frac{10!}{(10-4)!\cdot 4!}=\frac{10!}{6!\cdot 4!}=210. $$
Следовательно, общее количество искомых наборов равно 210.
Ответ : 210.
Сочетание с повторениями из $n$ элементов по $k$ – неупорядоченная $(n,k)$-выборка с повторениями.
Общее количество сочетаний с повторениями из $n$ элементов по $k$ определяется формулой:
\begin{equation}\bar{C}_{n}^{k}=\frac{(n+k-1)!}{(n-1)!\cdot k!} \end{equation}
Пример №6
Представьте себе, что мы находимся на конфетном заводе, - прямо возле конвейера, по которому движутся конфеты четырёх сортов. Мы запускаем руки в этот поток и вытаскиваем двадцать штук. Сколько всего различных "конфетных комбинаций" может оказаться в горсти?
Если принять, что первому сорту соответствует число 1, второму сорту - число 2 и так далее, то исходное множество в нашей задаче таково: $U=\{1,2,3,4\}$. Из этого множества мы выбираем 20 элементов (т.е., те самые 20 конфет с конвейера). Пригоршня конфет образует (4,20)-выборку. Естественно, повторения сортов будут. Вопрос в том, играет роль порядок расположения элементов в выборке или нет? Из условия задачи следует, что порядок расположения элементов роли не играет. Нам нет разницы, будут ли в горсти располагаться сначала 15 леденцов, а потом 4 шоколадных конфеты, или сначала 4 шоколадных конфеты, а уж потом 15 леденцов. Итак, мы имеем дело с неупорядоченной (4,20) выборкой с повторениями. Чтобы найти общее количество этих выборок используем формулу (6):
$$ \bar{C}_{4}^{20}=\frac{(4+20-1)!}{(4-1)!\cdot 20!}=\frac{23!}{3!\cdot 20!}=1771. $$
Следовательно, общее количество искомых комбинаций равно 1771.
Число сочетаний
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений .
Число сочетаний из n по k равно биномиальному коэффициенту

При фиксированном значении n производящей функцией чисел сочетаний с повторениями из n по k является:

Двумерной производящей функцией чисел сочетаний с повторениями является:
Wikimedia Foundation . 2010 .
70 семьдесят 67 · 68 · 69 · 70 · 71 · 72 · 73 40 · 50 · 60 · 70 · 80 · 90 · 100 Факторизация: 2×5×7 Римская запись: LXX Двоичное: 100 0110 … Википедия
Световое число, условное число, однозначно выражающее внеш. условия при фотосъёмке (обычно яркость объекта съёмки и светочувствительность применяемого фотоматериала). Любому значению Э. ч. можно подобрать неск. сочетаний диафрагменное число… … Большой энциклопедический политехнический словарь
Форма числа, выделяющая два предмета как по отношению к единичному предмету, так и по отношению к множеству предметов. В современном русском языке эта форма не существует, но остатки ее влияния сохранились. Так, сочетания два стола (ср. мн. ч.… … Словарь лингвистических терминов
Комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия
В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания… … Википедия
Занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера
1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия
- (греч. paradoxos неожиданный, странный) в широком смысле: утверждение, резко расходящееся с общепринятым, устоявшимся мнением, отрицание того, что представляется «безусловно правильным»; в более узком смысле два противоположных утверждения, для… … Философская энциклопедия
- (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия
Математическая теория, занимающаяся определением числа различных способов распределения данных предметов в известном порядке; имеет особенно важное значение в теории уравнений и в теории вероятностей. Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона