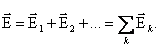
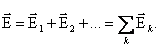
Een van de belangrijkste taken van elektrostatica is de evaluatie van veldparameters voor een gegeven, stationaire verdeling van ladingen in de ruimte. Een van de manieren om dergelijke problemen op te lossen is gebaseerd op superpositie principe . De essentie is als volgt.
Als een veld wordt gecreëerd door verschillende puntladingen, wordt de testvulling q uitgevoerd door de lading qk, alsof er geen andere ladingen zijn. De resulterende kracht wordt bepaald door de uitdrukking:
omdat , dan - de resulterende veldsterkte op het punt waar de proeflading zich ook bevindt gehoorzaamt aan het superpositieprincipe :
|
(1.4.1) |
Deze verhouding geeft het principe van superpositie weer of superpositie van elektrische velden en vertegenwoordigt een belangrijke eigenschap elektrisch veld. Spanning van het resulterende veldsysteem puntlasten gelijk aan de vectorsom van de sterkten van de velden die op een gegeven moment door elk afzonderlijk afzonderlijk zijn gemaakt.
Overweeg de toepassing van het superpositiebeginsel in het geval van een veld gecreëerd door een elektrisch systeem van twee ladingen met een afstand tussen ladingen gelijk aan l (fig. 1.2).
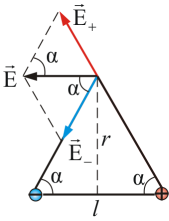
Fig. 1.2
De velden gemaakt met verschillende ladingen hebben geen invloed op elkaar, daarom kan de vector van het resulterende veld van verschillende kosten worden gevonden door de regel van toevoeging van vectoren (parallellogramregel)
 .
|
In dit geval
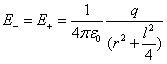en 
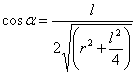
daarom,
 |
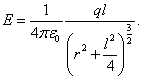(1.4.2) |
Overweeg een ander voorbeeld. Zoek de elektrostatische veldsterkte Egemaakt door twee positieve ladingen q 1 en q 2 op het punt Eengelegen op een afstand r 1 vanaf de eerste en r 2 van de tweede lading (fig. 1.3).
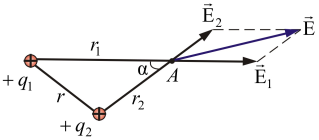
Fig. 1.3
We gebruiken de cosinusstelling:
| (1.4.3) |
waarin 
.
Als het veld is gemaakt geen puntladingen, gebruik dan de gebruikelijke techniek in dergelijke gevallen. Het lichaam is verdeeld in oneindig kleine elementen en bepaalt de veldsterkte die door elk element wordt gecreëerd en vervolgens door het hele lichaam wordt geïntegreerd:
| (1.4.4) |
Waar is de veldsterkte vanwege het geladen element. De integraal kan lineair zijn, in oppervlakte of in volume, afhankelijk van de vorm van het lichaam. Gebruik de juiste waarden voor ladingsdichtheid om dergelijke problemen op te lossen:
- lineaire ladingsdichtheid, gemeten in C / m;
- oppervlakteladingsdichtheid, gemeten in C / m2;
- bulkladingsdichtheid, gemeten in C / m3.
Als het veld wordt gemaakt door geladen lichamen met een complexe vorm en niet-uniform geladen, dan is het gebruik van het superpositiebeginsel moeilijk om het resulterende veld te vinden.
formule (1.4.4), zien we dat dit een vectorhoeveelheid is:
 |
(1.4.5) |
Integratie kan dus moeilijk zijn. Daarom worden vaak andere methoden gebruikt voor de berekening, die we in de volgende onderwerpen zullen bespreken. In sommige relatief eenvoudige gevallen kunnen deze formules echter analytisch worden berekend.
Als voorbeelden, overweeg lineaire ladingsverdeling of ladingsverdeling rond een cirkel.
Bepaal het elektrische veld op het punt Een (Fig. 1.4) op een afstand x van een oneindig lange, lineaire, uniform verdeelde lading. Laat λ de lading per lengte-eenheid zijn.
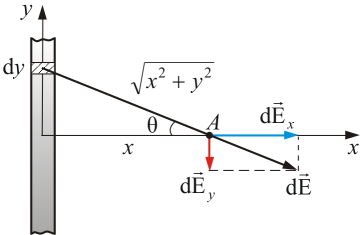
Fig. 1.4
Wij geloven dat x klein is in vergelijking met de lengte van de geleider. Kies een coördinatensysteem zodat de y-as samenvalt met de geleider. Lengte element dy, draagt een lading De elektrische veldintensiteit gecreëerd door dit element bij Een.
Elke elektrische lading verandert op een bepaalde manier de eigenschappen van de omringende ruimte - creëert elektrisch veld. Dit veld manifesteert zich in het feit dat een lading, op een bepaald punt geplaatst, een kracht ervaart. De ervaring leert dat de kracht die werkt op een vaste lading Q altijd kan worden weergegeven als: waar is de elektrische veldintensiteit. De veldsterkte wordt uitgedrukt in volt per meter (V / m). Experimentele feiten suggereren dat de veldsterkte van een systeem van zinloze vaste lasten gelijk is aan de vectorsom van de veldsterkten die elk van de kosten afzonderlijk zouden creëren:
Deze verklaring wordt het principe van superpositie van elektrische velden genoemd.
De vergelijkingen die het elektrostatische veld in een vacuüm beschrijven zijn: 
(1)
Is de vector van de elektrische veldsterkte, r is de ladingsdichtheid, e 0 is de elektrische constante.
Voor het elektrostatische veld is, in aanvulling op differentiaalvergelijkingen (1), de integraalrelatie, de Gauss-stelling genoemd, geldig.
Gauss-stelling. De stroom van een vector door een willekeurig gesloten oppervlak S is gelijk aan de algebraïsche som van de ladingen binnen dit oppervlak gedeeld door e0.
Deze stelling wordt gebruikt om velden met een symmetrische ladingsverdeling te berekenen. Bijvoorbeeld in het geval van een uniform geladen oneindige gloeidraad, een oneindige cilinder, een bol, een bal.
Een vectorveld waarvan de rotor nul is, wordt potentiaal genoemd. Het elektrostatische veld is potentieel, omdat
De krachtlijnen van het elektrostatische veld beginnen op positieve ladingen en eindigen op negatieve.
Krachtens (2) in een elektrostatisch veld, is het werk van de veldkrachten wanneer een lading van het ene punt naar het andere beweegt niet afhankelijk van de manier waarop deze beweging wordt gemaakt, maar hangt alleen af van de begin- en eindpunten van het pad.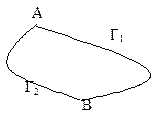 
Laten we het bewijzen.
Overweeg de beweging van punt A naar punt B langs het pad G 1 en het pad G 2. Het werk van de veldkrachten bij het verplaatsen van een enkele positieve lading op een gesloten lus bestaande uit paden G1 en G2 is gelijk aan
door de Stokes-stelling is deze integraal gelijk, waarbij S het oppervlak is dat over de betreffende contour gespannen is. Maar krachtens (2) == 0. Dus, = 
=
= 0, dat wil zeggen,
.
Omdat de gradientrotor altijd nul is, is de algemene oplossing van vergelijking (2) dat
Het minteken is van oudsher ontstaan, het heeft geen fundamentele betekenis. Maar dankzij dit teken, is de vector van spanning gericht op de vermindering van potentieel. De elektrostatische potentiaal j is gelijk aan de verhouding van de potentiële energie van de interactie van de lading met het veld tot de grootte van deze lading. Het potentiaalverschil tussen de twee punten van het veld, die de werking van het elektrostatische veld bepalen door ladingsoverdracht van het ene punt naar het andere, heeft een directe fysieke betekenis.
Het elektrostatische veld wordt beschreven door vergelijkingen (1) of door de Poisson-vergelijking voor de scalaire potentiaal j:
De oplossing van vergelijking (4) is:
(5)
Elektrisch veld is gemaakt elektrische ladingen of gewoon geladen lichamen, en werkt ook op deze objecten, ongeacht of ze bewegen of stilstaan. Als elektrisch geladen lichamen stationair zijn in een gegeven referentiekader, wordt hun interactie uitgevoerd door middel van een elektrostatisch veld. De krachten die werken op ladingen (geladen deeltjes) uit het elektrostatische veld worden elektrostatische krachten genoemd.
Het kwantitatieve kenmerk van de krachtwerking van het elektrische veld op geladen deeltjes en lichamen is de vectorhoeveelheid E, de elektrische veldsterkte genoemd.
Laten we de lading q beschouwen als de "bron" van het elektrische veld, waarin op een afstand r de eenheid proefopname q / = + 1, d.w.z. een lading die geen herverdeling van kosten veroorzaakt die het veld creëren. Dan, volgens de wet van Coulomb, zal de kracht op de testlading inwerken.
daarom, elektrostatische veldsterktevector op dit punt is numeriek gelijk aan kracht handelend op een proefeenheid positieve lading q / geplaatst op dit punt van het veld
waarin – radius is een vector van een puntlading naar een veld dat wordt bestudeerd. De eenheid van spanning is = /. De spanning wordt langs de straal geleid - de vector die wordt getekend vanaf het punt waar de lading zich bevindt, naar punt A (weg van de lading, als de lading positief is, en naar de lading - als de lading negatief is).
Een elektrisch veld wordt homogeen genoemd als de intensiteitsvector ervan hetzelfde is op alle punten van het veld, d.w.z. komt overeen zowel in module als in richting. Voorbeelden van dergelijke velden zijn elektrostatische velden van een uniform geladen oneindig vlak en platte condensator ver van de randen van zijn facings. Gebruik voor de grafische weergave van het elektrostatische veld de voedingslijnen ( spanningslijnen) - denkbeeldige lijnen, waarvan de raaklijnen samenvallen met de richting van de intensiteitsvector op elk punt van het veld (Fig. 10.4.- weergegeven door getrokken lijnen). De dichtheid van lijnen wordt bepaald door de spanningsmodulus op een bepaald punt in de ruimte.
Spanningslijnen zijn open - ze beginnen op positief en eindigen op negatieve ladingen. Elektrische leidingen ze kruisen nergens, omdat op elk punt van het veld de intensiteit ervan één enkele waarde en een bepaalde richting heeft.
Overweeg het elektrische veld van twee puntsladingen q 1 en q 2 .
 |
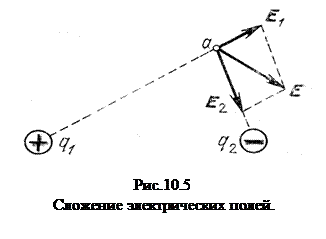De elektrische veldsterkte van verschillende ladingen is principe van superpositie van elektrostatische veldenvolgens welke de spanning het resulterende veld gecreëerd door het ladingsysteem is gelijk aan de meetkundige som van de veldsterkten gecreëerd op een bepaald punt door elk van de ladingen afzonderlijk.
